Binary Classification Model: Predicting Titanic Survivors with R

Using Tidymodels

1 Introduction

This document provides a comprehensive, step-by-step guide to building a binary classification model using the tidymodels ecosystem in R. We will tackle the classic Titanic dataset, a rich collection of passenger data, to predict survival. This project will walk you through the entire machine learning pipeline, from initial data loading and exploratory data analysis (EDA) to sophisticated model training, hyperparameter tuning, and final model evaluation and deployment.

The primary goal is to demonstrate a robust and reproducible workflow for classification tasks. We will explore various algorithms, compare their performance, and select the best model for making predictions on unseen data.

2 Installing and Loading Libraries

2.1 Step 1: Install Necessary Libraries

First, we ensure that all the required R packages are installed. We use the pak package for efficient and reliable package management.

Code

# This chunk installs all necessary packages. 
# It's set to not evaluate by default to avoid re-installing every time.
if (!requireNamespace("pak", quietly = TRUE)) {
  install.packages("pak")
}
# pak::pak handles dependencies gracefully.
pak::pak(c("tidymodels", "tidyverse", "titanic", "here", "naniar", "kableExtra", "ranger", "xgboost", "kknn", "kernlab", "doParallel", "discrim", "glmnet", "future.apply", "reactable", "skimr", "themis"))

2.2 Step 2: Load Libraries

Next, we load the libraries that will be used throughout the analysis. Each library serves a specific purpose, from data manipulation (tidyverse) to modeling (tidymodels) and creating interactive tables (reactable).

Code

library(tidymodels)      # Core package for modeling
library(tidyverse)       # Data manipulation and visualization
library(titanic)         # Contains the Titanic dataset
library(here)            # For reproducible file paths
library(naniar)          # For visualizing missing data
library(kableExtra)      # For creating beautiful tables
library(discrim)         # For discriminant analysis models
library(glmnet)          # For regularized regression models
library(reactable)       # For interactive tables
library(future)          # For parallel processing
library(skimr)           # For summary statistics
library(themis)          # For dealing with imbalanced data

3 Data Preparation

3.1 Step 3: Read Data

We load the Titanic dataset, which is stored in a CSV file. The here package helps in locating the file relative to the project’s root directory, making the code more portable.

Code

titanic_df <- read_csv(here("./data", "titanic_data.csv"))

# Glimpse the data to see its structure and variable types
glimpse(titanic_df)

Rows: 891
Columns: 12
$ PassengerId <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,…
$ Survived    <dbl> 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1…
$ Pclass      <dbl> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3, 2, 3, 3…
$ Name        <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bradley (Fl…
$ Sex         <chr> "male", "female", "female", "female", "male", "male", "mal…
$ Age         <dbl> 22, 38, 26, 35, 35, NA, 54, 2, 27, 14, 4, 58, 20, 39, 14, …
$ SibSp       <dbl> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4, 0, 1, 0…
$ Parch       <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1, 0, 0, 0…
$ Ticket      <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "113803", "37…
$ Fare        <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, 51.8625,…
$ Cabin       <chr> NA, "C85", NA, "C123", NA, NA, "E46", NA, NA, NA, "G6", "C…
$ Embarked    <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", "S", "S"…

3.2 Step 4: Exploratory Data Analysis (EDA)

EDA is a crucial step to understand the data’s underlying structure, identify missing values, and uncover relationships between variables.

Code

# Get a quick summary of the dataset
summary(titanic_df)

  PassengerId       Survived          Pclass          Name          
 Min.   :  1.0   Min.   :0.0000   Min.   :1.000   Length:891        
 1st Qu.:223.5   1st Qu.:0.0000   1st Qu.:2.000   Class :character  
 Median :446.0   Median :0.0000   Median :3.000   Mode  :character  
 Mean   :446.0   Mean   :0.3838   Mean   :2.309                     
 3rd Qu.:668.5   3rd Qu.:1.0000   3rd Qu.:3.000                     
 Max.   :891.0   Max.   :1.0000   Max.   :3.000                     
                                                                    
     Sex                 Age            SibSp           Parch       
 Length:891         Min.   : 0.42   Min.   :0.000   Min.   :0.0000  
 Class :character   1st Qu.:20.12   1st Qu.:0.000   1st Qu.:0.0000  
 Mode  :character   Median :28.00   Median :0.000   Median :0.0000  
                    Mean   :29.70   Mean   :0.523   Mean   :0.3816  
                    3rd Qu.:38.00   3rd Qu.:1.000   3rd Qu.:0.0000  
                    Max.   :80.00   Max.   :8.000   Max.   :6.0000  
                    NA's   :177                                     
    Ticket               Fare           Cabin             Embarked        
 Length:891         Min.   :  0.00   Length:891         Length:891        
 Class :character   1st Qu.:  7.91   Class :character   Class :character  
 Mode  :character   Median : 14.45   Mode  :character   Mode  :character  
                    Mean   : 32.20                                        
                    3rd Qu.: 31.00                                        
                    Max.   :512.33

Code

# Use skimr for more detailed and user-friendly summary statistics
skim(titanic_df)

Data summary
Name	titanic_df
Number of rows	891
Number of columns	12
_______________________
Column type frequency:
character	5
numeric	7
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	n_unique
Name	0	1.00	12	82	891
Sex	0	1.00	4	6	2
Ticket	0	1.00	3	18	681
Cabin	687	0.23	1	15	147
Embarked	2	1.00	1	1	3

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
PassengerId	0	1.0	446.00	257.35	1.00	223.50	446.00	668.5	891.00	▇▇▇▇▇
Survived	0	1.0	0.38	0.49	0.00	0.00	0.00	1.0	1.00	▇▁▁▁▅
Pclass	0	1.0	2.31	0.84	1.00	2.00	3.00	3.0	3.00	▃▁▃▁▇
Age	177	0.8	29.70	14.53	0.42	20.12	28.00	38.0	80.00	▂▇▅▂▁
SibSp	0	1.0	0.52	1.10	0.00	0.00	0.00	1.0	8.00	▇▁▁▁▁
Parch	0	1.0	0.38	0.81	0.00	0.00	0.00	0.0	6.00	▇▁▁▁▁
Fare	0	1.0	32.20	49.69	0.00	7.91	14.45	31.0	512.33	▇▁▁▁▁

3.2.1 Automated EDA with `DataExplorer`

The DataExplorer package can generate a comprehensive HTML report, providing a deep dive into the data with a single command.

Code

# This command generates a detailed EDA report.
create_report(titanic_df, y = "Survived")

3.2.2 Visualizing Missing Data and Key Relationships

Code

# Visualize missing data to understand its extent
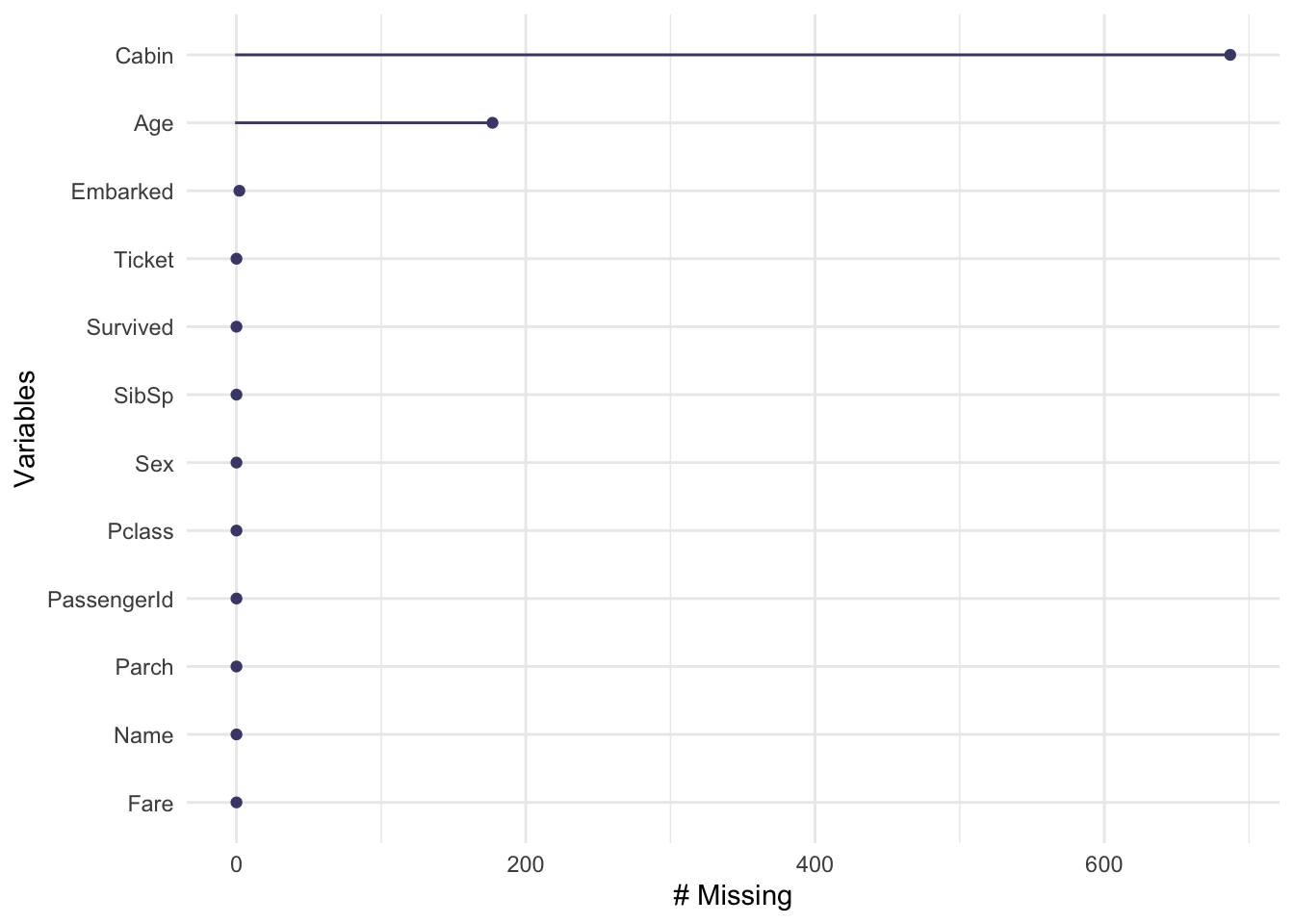
gg_miss_var(titanic_df)

Code

# Explore survival rate by passenger class
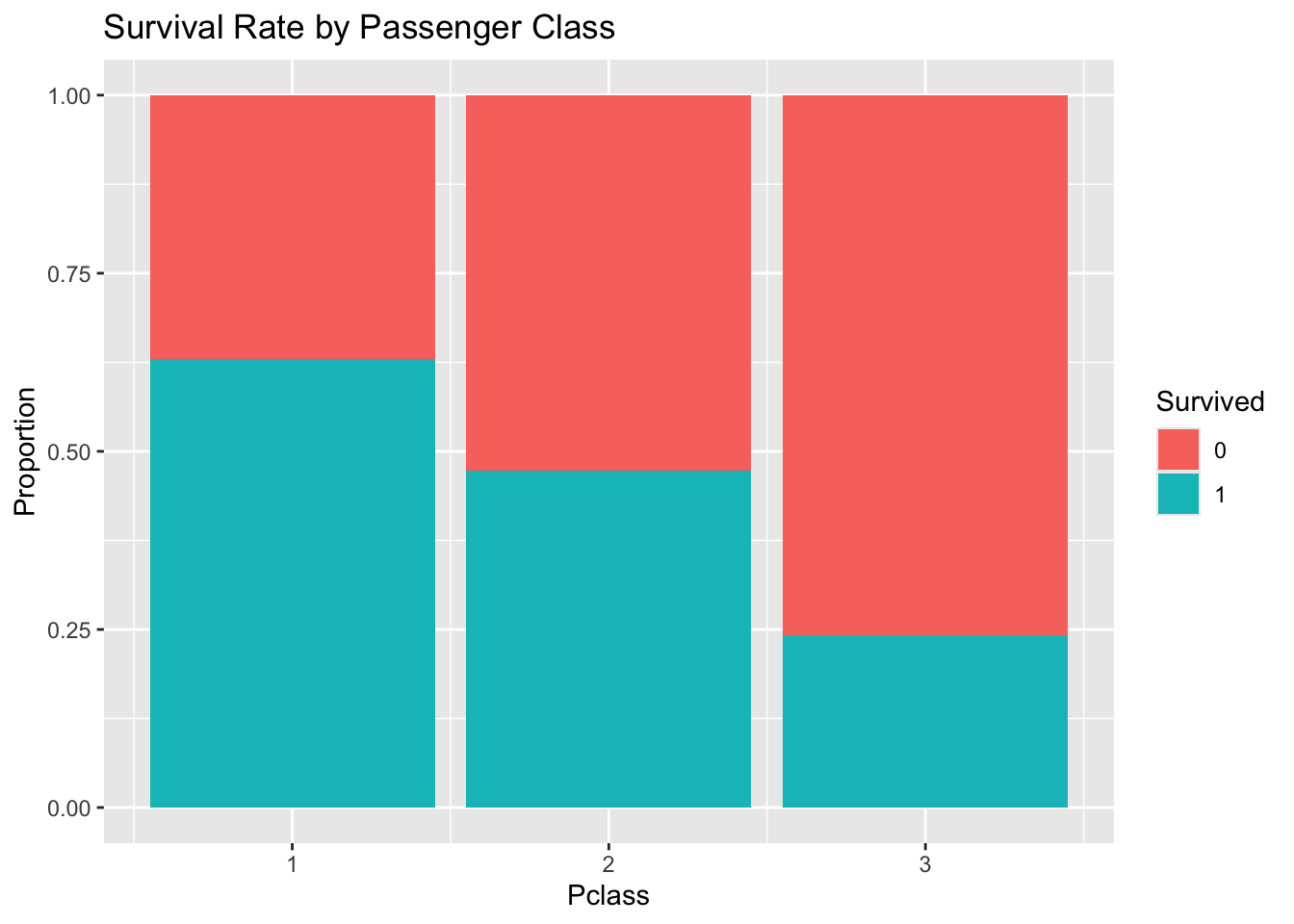
titanic_df %>%
  mutate(Survived = as.factor(Survived)) %>%
  ggplot(aes(x = Pclass, fill = Survived)) +
  geom_bar(position = "fill") +
  labs(y = "Proportion", title = "Survival Rate by Passenger Class")

Code

# Explore survival rate by sex
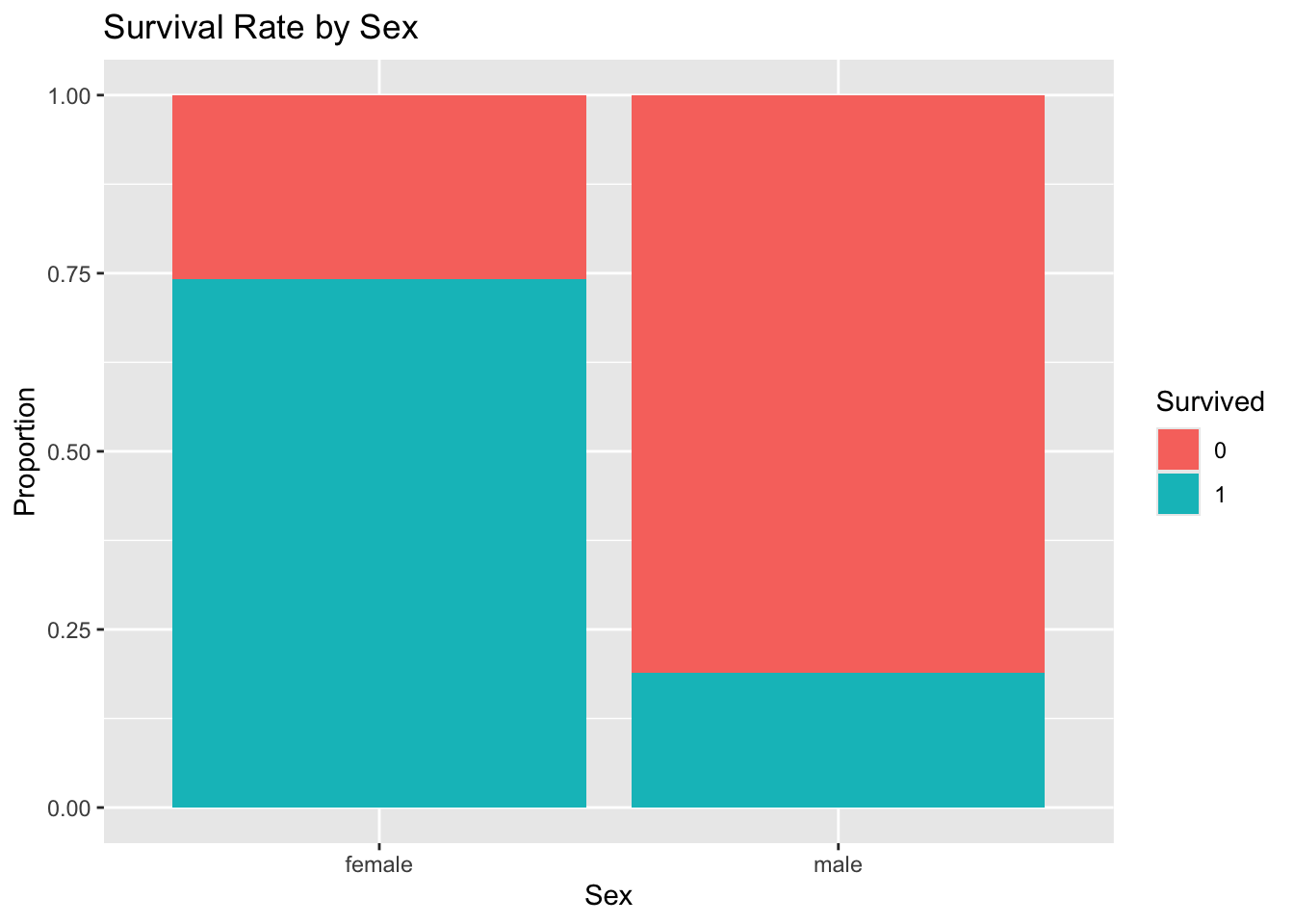
titanic_df %>%
  mutate(Survived = as.factor(Survived)) %>%
  ggplot(aes(x = Sex, fill = Survived)) +
  geom_bar(position = "fill") +
  labs(y = "Proportion", title = "Survival Rate by Sex")

Code

# Explore age distribution by survival
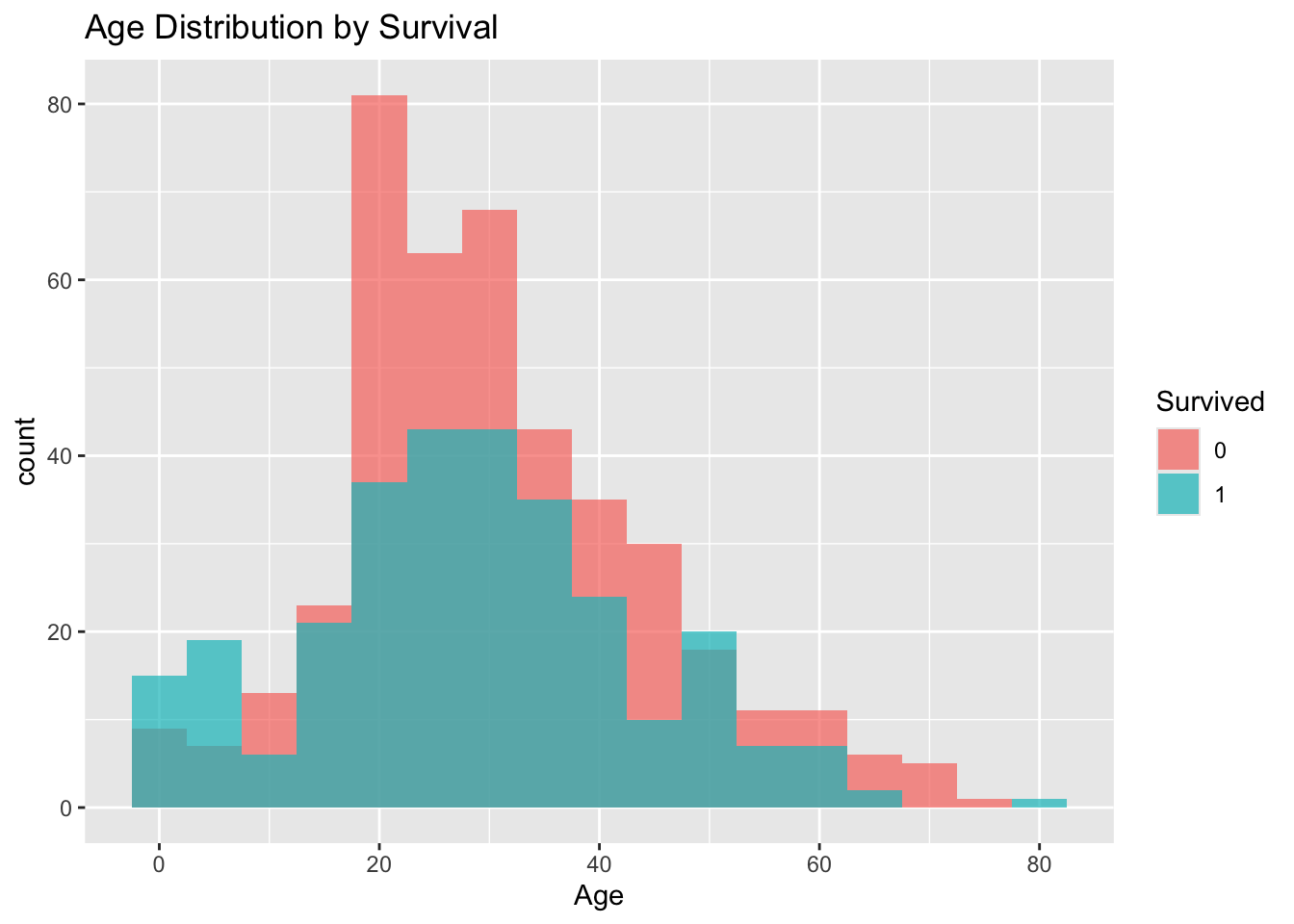
titanic_df %>%
  mutate(Survived = as.factor(Survived)) %>%
  ggplot(aes(x = Age, fill = Survived)) +
  geom_histogram(binwidth = 5, position = "identity", alpha = 0.7) +
  labs(title = "Age Distribution by Survival")

3.3 Step 5: Data Cleaning and Feature Engineering

We perform some initial data cleaning, such as converting variables to the correct type. More complex preprocessing will be handled by the recipe.

Code

titanic_clean <- titanic_df %>%
  mutate(
    Survived = as.factor(Survived),
    Pclass = as.factor(Pclass)
  ) %>%
  select(Survived, Pclass, Sex, Age, SibSp, Parch, Fare, Embarked, PassengerId, Name, Ticket)

titanic_clean$Pclass <- as.factor(titanic_clean$Pclass)
glimpse(titanic_clean)

Rows: 891
Columns: 11
$ Survived    <fct> 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1…
$ Pclass      <fct> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3, 2, 3, 3…
$ Sex         <chr> "male", "female", "female", "female", "male", "male", "mal…
$ Age         <dbl> 22, 38, 26, 35, 35, NA, 54, 2, 27, 14, 4, 58, 20, 39, 14, …
$ SibSp       <dbl> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4, 0, 1, 0…
$ Parch       <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1, 0, 0, 0…
$ Fare        <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, 51.8625,…
$ Embarked    <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", "S", "S"…
$ PassengerId <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,…
$ Name        <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bradley (Fl…
$ Ticket      <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "113803", "37…

3.3.1 Variable Groups

Target Variable: Survived
Numerical Features: Age, SibSp, Parch, Fare
Categorical Features: Pclass, Sex, Embarked
Identifier Variables: PassengerId, Name, Ticket (to be excluded from modeling)

3.4 Step 6: Data Splitting

To properly evaluate our models, we split the data into three sets: a training set (for model building), a testing set (for tuning and initial evaluation), and a final hold-out set (for unbiased final validation).

Code

set.seed(123) # for reproducibility

# First, split into training/testing (90%) and hold-out (10%)
split_ho <- initial_split(titanic_clean, prop = 0.9, strata = Survived)
train_test_data <- training(split_ho)
holdout_data <- testing(split_ho)

# Next, split the 90% into training (7/9) and testing (2/9)
# This results in overall proportions of 70% train, 20% test
split_tt <- initial_split(train_test_data, prop = 7/9, strata = Survived)
train_data <- training(split_tt)
test_data <- testing(split_tt)

# Create cross-validation folds from the training data for robust evaluation
folds <- vfold_cv(train_data, v = 5, strata = Survived)

# Check the proportions of each dataset
cat("Training data:", nrow(train_data), "rows
")

Training data: 622 rows

Code

cat("Testing data:", nrow(test_data), "rows
")

Testing data: 179 rows

Code

cat("Hold-out data:", nrow(holdout_data), "rows
")

Hold-out data: 90 rows

Code

saveRDS(train_data, here("./data", "train_data.rds"))
saveRDS(test_data, here("./data", "test_data.rds"))
saveRDS(holdout_data, here("./data", "holdout_data.rds"))

4 Modeling

4.1 Step 7: Create a Preprocessing Recipe

A recipe is a powerful tool from tidymodels for defining a sequence of data preprocessing steps. This ensures that the same transformations are applied consistently to all data splits.

Our recipe will: - Impute missing Age values using K-Nearest Neighbors. - Impute missing Embarked values using the mode. - Create dummy variables for all categorical predictors. - Normalize all numeric predictors to have a mean of 0 and standard deviation of 1. - Assign identifier roles to columns that should not be used as predictors.

Code

titanic_recipe <- recipe(Survived ~ ., data = train_data) %>%
  update_role(c(PassengerId, Name, Ticket), new_role = "sample ID") %>%
  step_impute_knn(Age, neighbors = 5) %>%
  step_impute_mode(Embarked) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_normalize(all_numeric_predictors())

# Check the recipe to see the transformations
summary(prep(titanic_recipe))

# A tibble: 13 × 4
   variable    type      role      source  
   <chr>       <list>    <chr>     <chr>   
 1 Age         <chr [2]> predictor original
 2 SibSp       <chr [2]> predictor original
 3 Parch       <chr [2]> predictor original
 4 Fare        <chr [2]> predictor original
 5 PassengerId <chr [2]> sample ID original
 6 Name        <chr [3]> sample ID original
 7 Ticket      <chr [3]> sample ID original
 8 Survived    <chr [3]> outcome   original
 9 Pclass_X2   <chr [2]> predictor derived 
10 Pclass_X3   <chr [2]> predictor derived 
11 Sex_male    <chr [2]> predictor derived 
12 Embarked_Q  <chr [2]> predictor derived 
13 Embarked_S  <chr [2]> predictor derived

Code

# Bake the recipe to see the transformed data
titanic_recipe %>% prep() %>% bake(new_data = test_data) %>% head() %>% glimpse()

Rows: 6
Columns: 13
$ Age         <dbl> -0.15027135, 0.05750583, -1.86980665, -0.29356596, -0.3508…
$ SibSp       <dbl> 0.5048153, -0.4352898, 2.3850256, 0.5048153, -0.4352898, 0…
$ Parch       <dbl> -0.4690643, -0.4690643, 2.1953921, -0.4690643, -0.4690643,…
$ Fare        <dbl> 1.11363266, -0.50395531, -0.07075544, -0.36419216, -0.5073…
$ PassengerId <dbl> 35, 46, 64, 74, 77, 87
$ Name        <chr> "Meyer, Mr. Edgar Joseph", "Rogers, Mr. William John", "Sk…
$ Ticket      <chr> "PC 17604", "S.C./A.4. 23567", "347088", "2680", "349208",…
$ Survived    <fct> 0, 0, 0, 0, 0, 0
$ Pclass_X2   <dbl> -0.5235921, -0.5235921, -0.5235921, -0.5235921, -0.5235921…
$ Pclass_X3   <dbl> -1.1078873, 0.9011678, 0.9011678, 0.9011678, 0.9011678, 0.…
$ Sex_male    <dbl> 0.7236481, 0.7236481, 0.7236481, 0.7236481, 0.7236481, 0.7…
$ Embarked_Q  <dbl> -0.320424, -0.320424, -0.320424, -0.320424, -0.320424, -0.…
$ Embarked_S  <dbl> -1.5239630, 0.6551289, 0.6551289, -1.5239630, 0.6551289, 0…

4.2 Step 8: Define Models

We will define a suite of classification models to compare their performance on this dataset.

4.2.1 Model Introductions

Logistic Regression: A linear model that predicts the probability of a binary outcome. It’s simple, interpretable, and a great baseline.
K-Nearest Neighbors (KNN): A non-parametric algorithm that classifies a data point based on the majority class of its ‘k’ nearest neighbors.
Support Vector Machines (SVM): A model that finds an optimal hyperplane to separate classes in the feature space. We’ll use a radial basis function kernel.
Decision Trees: A tree-like model of decisions. Simple to understand and visualize, but can be prone to overfitting.
Random Forest: An ensemble of many decision trees. It improves upon single trees by averaging their results, reducing overfitting and increasing accuracy. We will tune its hyperparameters.
XGBoost: An advanced and highly efficient implementation of gradient boosting. It’s known for its high performance and is a popular choice in competitions. We will tune its hyperparameters.
Neural Networks: A model inspired by the human brain, consisting of interconnected nodes (neurons) in layers. It can capture complex non-linear relationships.
Naive Bayes: A probabilistic classifier based on Bayes’ theorem with a ‘naive’ assumption of conditional independence between features. It is very fast and works well with high-dimensional data.
Regularized Logistic Regression: An extension of logistic regression that includes a penalty term (L1/Lasso or L2/Ridge) to prevent overfitting by shrinking coefficient estimates. We will tune the penalty and mixture parameters.

4.2.2 Model Specifications

Code

# Logistic Regression
log_reg_spec <- logistic_reg() %>%
  set_engine("glm") %>%
  set_mode("classification")

# K-Nearest Neighbors
knn_spec <- nearest_neighbor() %>%
  set_engine("kknn") %>%
  set_mode("classification")

# Support Vector Machine
svm_spec <- svm_rbf() %>%
  set_engine("kernlab") %>%
  set_mode("classification")

# Decision Tree
tree_spec <- decision_tree() %>%
  set_engine("rpart") %>%
  set_mode("classification")

# Random Forest (Tunable)
rf_spec <- rand_forest(
  mtry = tune(),
  trees = tune(),
  min_n = tune()
) %>%
  set_engine("ranger") %>%
  set_mode("classification")

# XGBoost (Tunable)
xgb_spec <- boost_tree(
  trees = tune(),
  tree_depth = tune(),
  min_n = tune(),
  learn_rate = tune(),
  loss_reduction = tune()
) %>%
  set_engine("xgboost") %>%
  set_mode("classification")

# Neural Network
nn_spec <- mlp(hidden_units = tune(), penalty = tune(), epochs = 100) %>%
    set_engine("nnet") %>%
    set_mode("classification")

# Naive Bayes
nb_spec <- naive_Bayes() %>%
  set_engine("naivebayes") %>%
  set_mode("classification")

# Regularized Logistic Regression (Tunable)
glmnet_spec <- logistic_reg(penalty = tune(), mixture = tune()) %>%
  set_engine("glmnet") %>%
  set_mode("classification")

4.2.3 Model Comparison Table

Model	Key Strengths	Key Weaknesses	Tunable
Logistic Regression	Interpretable, fast, good baseline	Assumes linearity	No
K-Nearest Neighbors	Simple, non-parametric	Computationally intensive, needs scaling	No
SVM	Effective in high dimensions, robust	Can be slow, less interpretable	No
Decision Tree	Easy to interpret and visualize	Prone to overfitting	No
Random Forest	High accuracy, robust to overfitting	Less interpretable, can be slow	Yes
XGBoost	Top-tier performance, fast, flexible	Complex, many parameters to tune	Yes
Neural Network	Captures complex patterns, highly flexible	Requires large data, prone to overfitting	Yes
Naive Bayes	Very fast, works well on wide data	Strong feature independence assumption	No
Regularized Logistic Regression	Prevents overfitting, feature selection (Lasso)	Less interpretable than simple LR	Yes

4.3 Step 9: Create a WorkflowSet

A workflow_set is a powerful and convenient way to manage multiple workflows (recipe + model combinations) simultaneously, making it easy to train and compare them.

Code

all_models <- list(
    log_reg = log_reg_spec,
    knn = knn_spec,
    svm = svm_spec,
    tree = tree_spec,
    rf = rf_spec,
    xgb = xgb_spec,
    nn = nn_spec,
    nb = nb_spec,
    glmnet = glmnet_spec
)

all_workflows <- workflow_set(
  preproc = list(recipe = titanic_recipe),
  models = all_models
)

4.4 Step 10: Training and Hyperparameter Tuning

We use workflow_map() to efficiently fit the non-tunable models and tune the hyperparameters for the tunable ones using grid search. We’ll leverage parallel processing to speed up this step.

Code

# Set up parallel processing to speed up computation
plan(multisession)

# Define the metrics we want to track
class_metrics <- metric_set(accuracy, roc_auc, sensitivity, precision)

# Tune the workflows using the cross-validation folds
set.seed(234)
tune_results <- workflow_map(
  all_workflows,
  "tune_grid",
  resamples = folds,
  grid = 15, # Use a grid of 15 candidate parameter sets for tuning
  metrics = class_metrics,
  control = control_grid(save_pred = TRUE) # Save predictions for later analysis
)

5 Model Evaluation

5.1 Step 11: Compare Model Performance

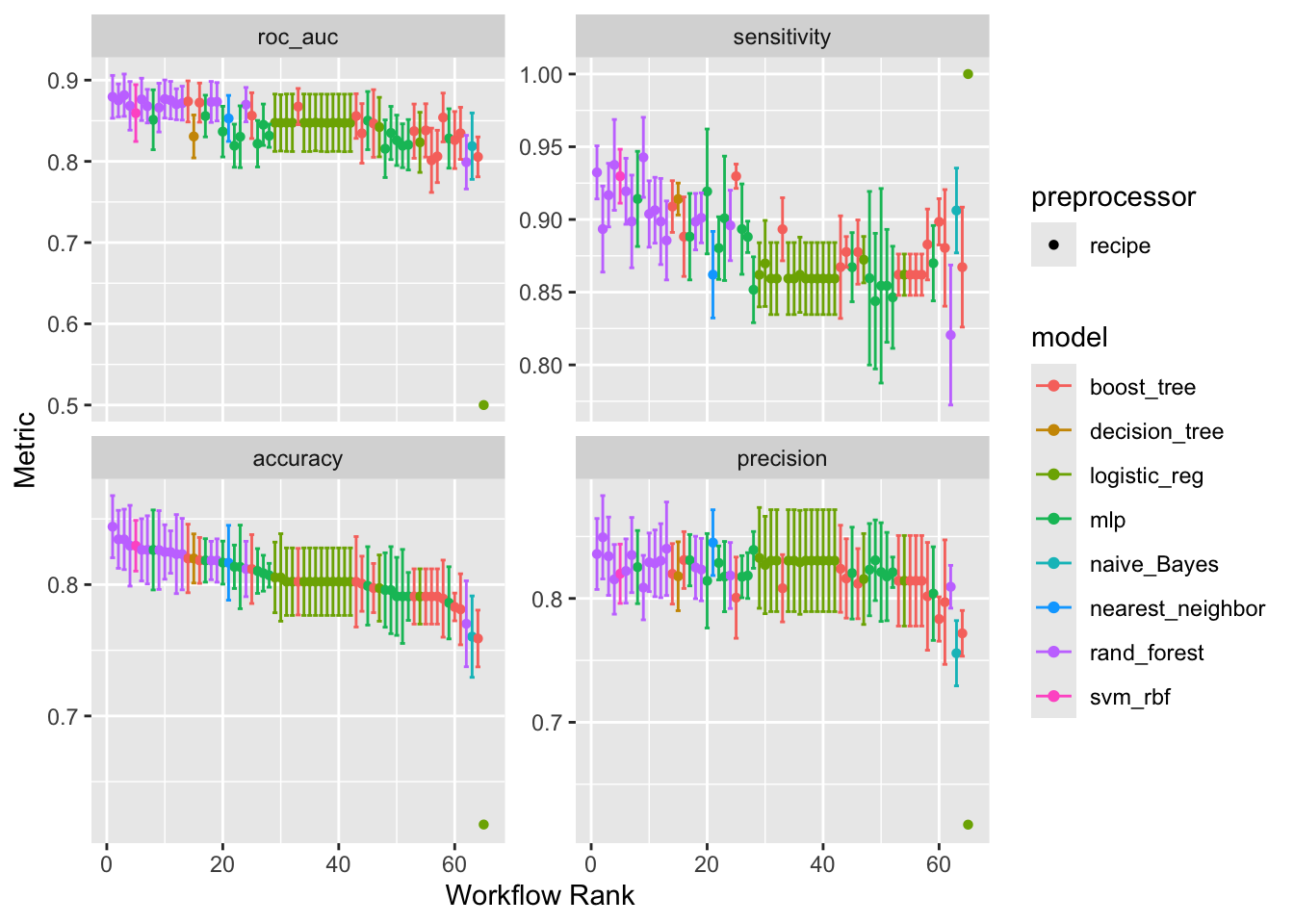
Let’s visualize and compare the performance of all our trained models.

Code

# Plot the results to visually compare model performance across metrics
autoplot(tune_results)

5.1.1 Understanding the Metrics

Before diving into the results, it’s crucial to understand what each metric signifies. For binary classification, we often use a confusion matrix to evaluate a model’s performance.

	Predicted: Survived	Predicted: Perished
Actual: Survived	True Positive (TP)	False Negative (FN)
Actual: Perished	False Positive (FP)	True Negative (TN)

AUC - ROC (Area Under the Receiver Operating Characteristic Curve): This is a key metric for classification. It measures the model’s ability to distinguish between classes. An AUC of 1.0 is a perfect model, while 0.5 is no better than random chance.
Accuracy: The proportion of correct predictions. It can be misleading if classes are imbalanced. (TP + TN) / (TP + TN + FP + FN)
Precision: Of all passengers predicted to survive, how many actually did? TP / (TP + FP)
Recall (Sensitivity): Of all passengers who actually survived, how many did our model correctly identify? TP / (TP + FN)

Code

# Rank models by accuracy and display in an interactive table
rank_results(tune_results, rank_metric = "accuracy") %>%
  filter(.metric == "accuracy") %>%
  select(-n, -std_err, -preprocessor) %>%
  reactable(
    defaultPageSize = 10,
    striped = TRUE,
    highlight = TRUE,
    compact = TRUE,
    columns = list(
      wflow_id = colDef(name = "Workflow"),
      .metric = colDef(name = "Metric"),
      mean = colDef(name = "Mean", format = colFormat(digits = 4)),
      rank = colDef(name = "Rank")
    ),
    defaultSorted = list(rank = "asc")
  )

Code

# Collect all metrics for further analysis
all_metrics <- collect_metrics(tune_results)

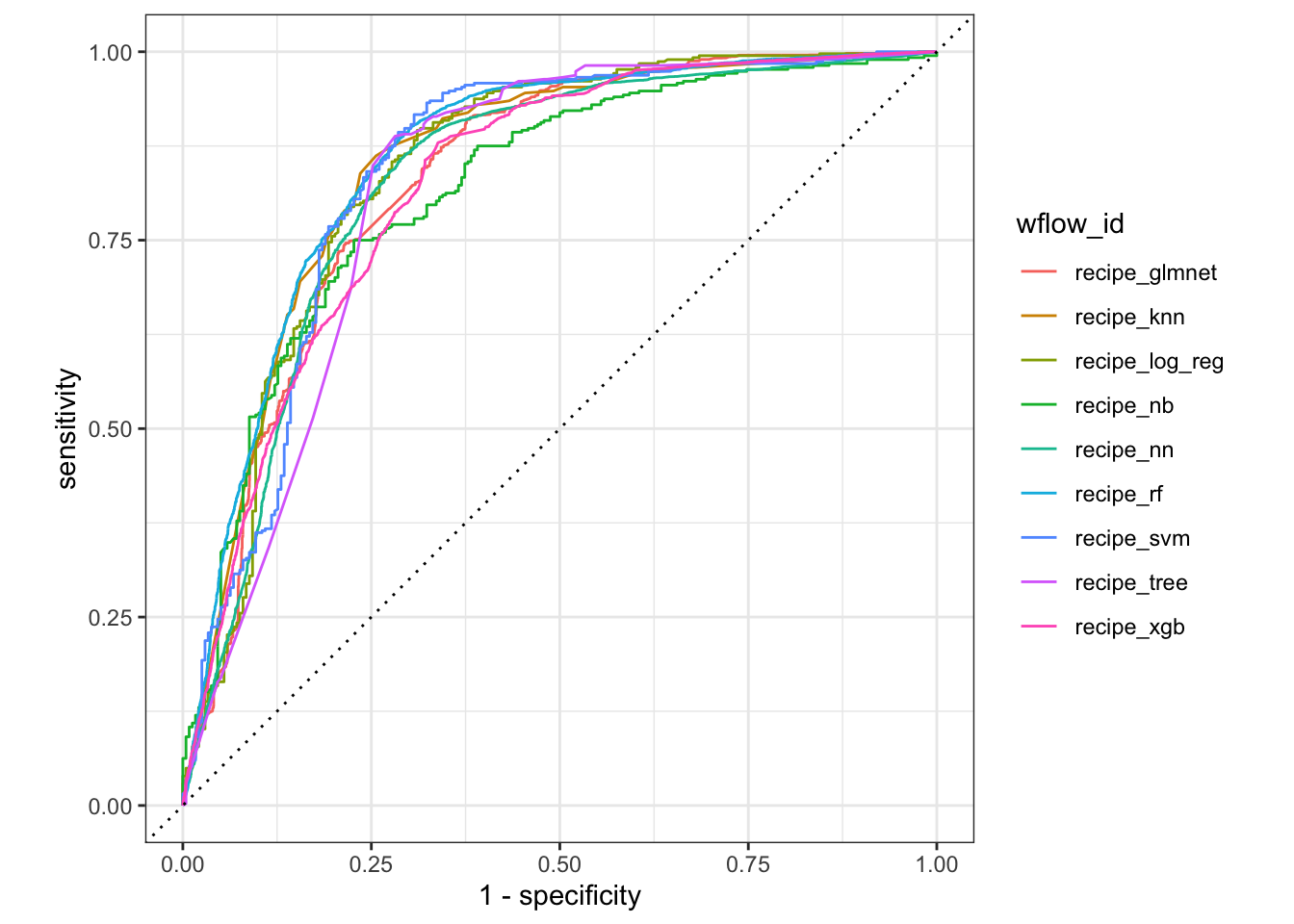
5.1.2 ROC Curves

We can plot the ROC curves for each model to visualize the trade-off between the true positive rate and the false positive rate.

Code

tune_results %>%
  collect_predictions() %>%
  group_by(wflow_id) %>%
  roc_curve(truth = Survived, .pred_0) %>%
  autoplot()

6 Finalizing and Deploying the Model

6.1 Step 12: Select and Save the Best Model

Based on our evaluation, XGBoost performed the best. We will now select this model, find its optimal hyperparameters, and fit it to the entire training and testing dataset.

Code

# Select the best workflow based on accuracy
best_wflow_id <- rank_results(tune_results, rank_metric = "accuracy") %>%
  dplyr::slice(1) %>%
  pull(wflow_id)

best_workflow <- extract_workflow(tune_results, id = best_wflow_id)

# Find the best hyperparameters for the top model
best_result <- extract_workflow_set_result(tune_results, id = best_wflow_id)
best_params <- select_best(best_result, metric = "accuracy")

best_params

# A tibble: 1 × 4
   mtry trees min_n .config              
  <int> <int> <int> <chr>                
1     2  1571    10 Preprocessor1_Model03

Code

# Finalize the workflow with the best parameters
final_workflow <- finalize_workflow(best_workflow, best_params)
final_workflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: rand_forest()

── Preprocessor ────────────────────────────────────────────────────────────────
4 Recipe Steps

• step_impute_knn()
• step_impute_mode()
• step_dummy()
• step_normalize()

── Model ───────────────────────────────────────────────────────────────────────
Random Forest Model Specification (classification)

Main Arguments:
  mtry = 2
  trees = 1571
  min_n = 10

Computational engine: ranger

Code

# Fit the final model on the combined training and testing data
final_fit <- fit(final_workflow, data = train_test_data)

# Save the final fitted workflow including

# the fitted model
# the preprocessor (recipe)
# everything needed to predict

saveRDS(final_fit, file = here("./model/best_titanic_model.rds"))

6.2 Step 13: Load the Saved Model

We can now load the saved model object for deployment or future predictions.

Code

loaded_model <- readRDS(here("./model/best_titanic_model.rds"))
#print(loaded_model)
summary(loaded_model)

        Length Class      Mode   
pre     3      stage_pre  list   
fit     2      stage_fit  list   
post    1      stage_post list   
trained 1      -none-     logical

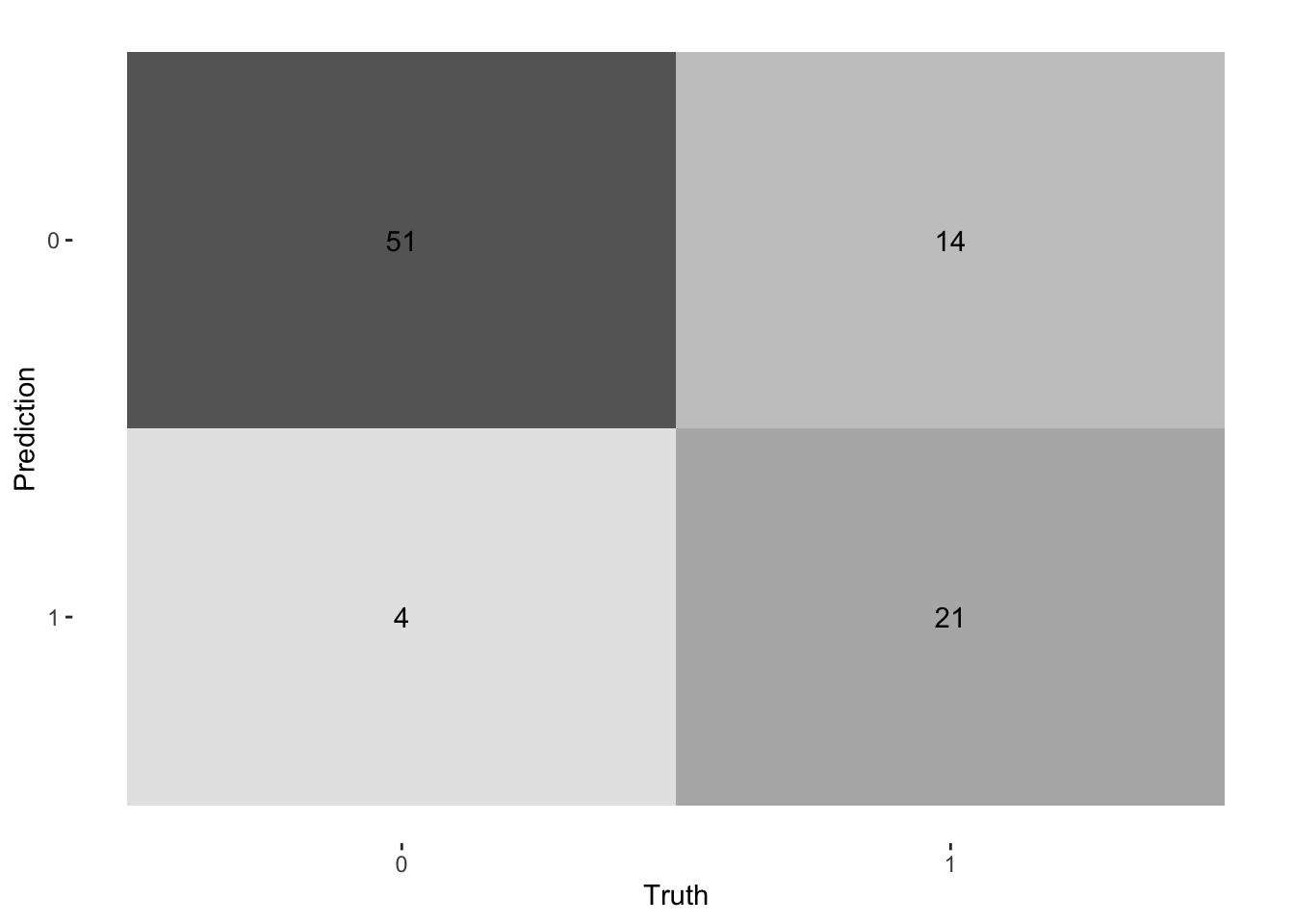
6.3 Step 14: Make Predictions on Hold-out Data

Finally, we evaluate our best model on the hold-out data, which it has never seen before. This provides the most realistic estimate of its performance on new, unseen data.

Code

# Make predictions on the hold-out set
holdout_predictions <- predict(loaded_model, new_data = holdout_data) %>%
  bind_cols(predict(loaded_model, new_data = holdout_data, type = "prob")) %>%
  bind_cols(holdout_data %>% select(Survived))

# Calculate performance metrics on the hold-out data
metrics <- metric_set(accuracy, precision, recall, f_meas, roc_auc)
final_performance <- metrics(holdout_predictions, truth = Survived, estimate = .pred_class, .pred_0)

# Display the final performance in a clean table
final_performance %>%
  kbl(caption = "Final Model Performance on Hold-out Data") %>%
  kable_styling(bootstrap_options = "striped", full_width = FALSE)

Final Model Performance on Hold-out Data
.metric	.estimator	.estimate
accuracy	binary	0.8000000
precision	binary	0.7846154
recall	binary	0.9272727
f_meas	binary	0.8500000
roc_auc	binary	0.8576623

Code

# Visualize the confusion matrix
conf_mat(holdout_predictions, truth = Survived, estimate = .pred_class) %>%
  autoplot(type = "heatmap")

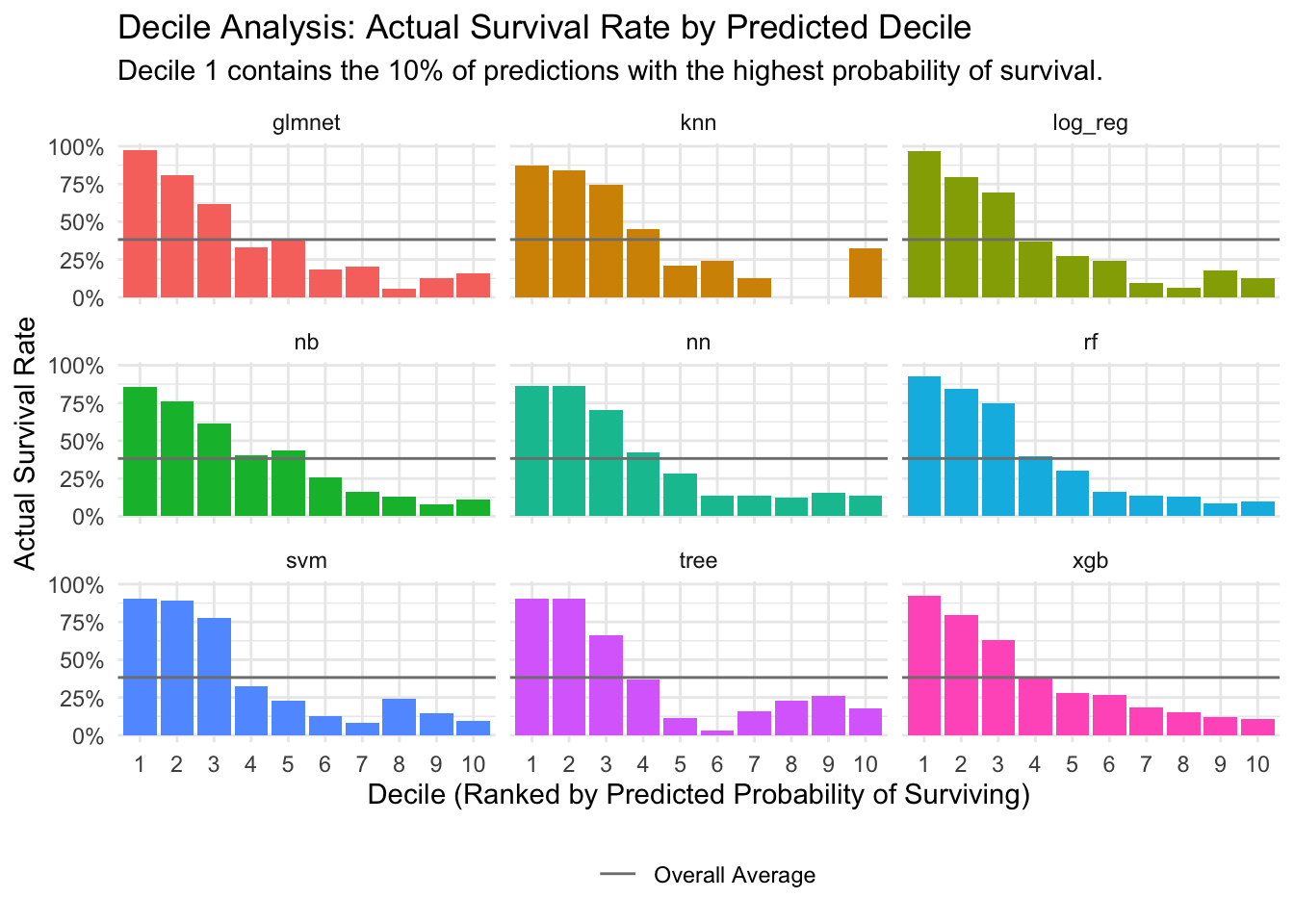
6.4 Step 15: Decile Analysis

To better understand how well our models discriminate between classes, we perform a decile analysis. We sort predictions by the probability of survival, group them into 10 deciles, and then calculate the actual survival rate within each decile. This helps to visualize if the models are effectively identifying high-risk and low-risk groups.

Code

# Get predictions from all models on the test set
all_predictions <- tune_results %>%
  collect_predictions()

# Calculate the overall average survival rate
overall_avg_survival <- mean(as.numeric(as.character(all_predictions$Survived)))

# Calculate deciles and survival rates for each model
decile_data <- all_predictions %>%
  mutate(Survived_numeric = as.numeric(as.character(Survived))) %>%
  group_by(wflow_id) %>%
  mutate(decile = ntile(desc(.pred_1), 10)) %>%
  group_by(wflow_id, decile) %>%
  summarise(
    avg_pred_prob = mean(.pred_1),
    actual_survival_rate = mean(Survived_numeric),
    n = n(),
    .groups = "drop"
  ) %>%
  mutate(wflow_id = str_remove(wflow_id, "recipe_"))

# Visualize the decile analysis
ggplot(decile_data, aes(x = as.factor(decile), y = actual_survival_rate)) +
  geom_col(aes(fill = wflow_id), show.legend = FALSE) +
  geom_hline(aes(yintercept = overall_avg_survival, linetype = "Overall Average"), color = "gray50") +
  scale_y_continuous(labels = scales::percent) +
  facet_wrap(~wflow_id, ncol = 3) +
  labs(
    title = "Decile Analysis: Actual Survival Rate by Predicted Decile",
    subtitle = "Decile 1 contains the 10% of predictions with the highest probability of survival.",
    x = "Decile (Ranked by Predicted Probability of Surviving)",
    y = "Actual Survival Rate",
    linetype = ""
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")

7 Conclusion

In this analysis, we successfully built and evaluated multiple machine learning models to predict Titanic survivors. The tidymodels framework provided a powerful and organized workflow for this task. Our final XGBoost model demonstrated strong performance on the hold-out data, indicating its effectiveness in this classification problem. This project serves as a template for tackling similar binary classification challenges in a structured and reproducible manner.

1 Introduction

2 Installing and Loading Libraries

2.1 Step 1: Install Necessary Libraries

2.2 Step 2: Load Libraries

3 Data Preparation

3.1 Step 3: Read Data

3.2 Step 4: Exploratory Data Analysis (EDA)

3.2.1 Automated EDA with DataExplorer

3.2.2 Visualizing Missing Data and Key Relationships

3.3 Step 5: Data Cleaning and Feature Engineering

3.3.1 Variable Groups

3.4 Step 6: Data Splitting

4 Modeling

4.1 Step 7: Create a Preprocessing Recipe

4.2 Step 8: Define Models

4.2.1 Model Introductions

4.2.2 Model Specifications

4.2.3 Model Comparison Table

4.3 Step 9: Create a WorkflowSet

4.4 Step 10: Training and Hyperparameter Tuning

5 Model Evaluation

5.1 Step 11: Compare Model Performance

5.1.1 Understanding the Metrics

5.1.2 ROC Curves

6 Finalizing and Deploying the Model

6.1 Step 12: Select and Save the Best Model

6.2 Step 13: Load the Saved Model

6.3 Step 14: Make Predictions on Hold-out Data

6.4 Step 15: Decile Analysis

7 Conclusion

3.2.1 Automated EDA with `DataExplorer`